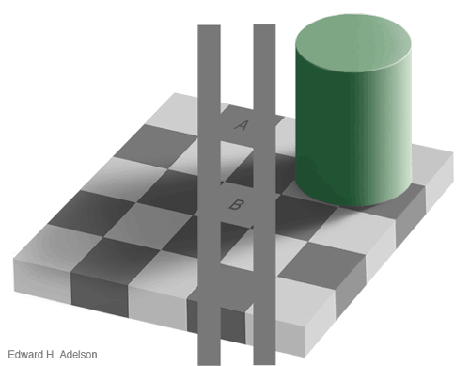
1. Tabuleiro de Adelson:
Os quadrados A e B são da mesma cor.
Vamos conferir:
2. Os círculos abaixo não estão tortos.
3. Grade de Hermann:
Há somente faixas brancas entre os quadrados. As manchas cinzas são uma ilusão.
4. Grade cintilante:
Nesta ilusão, que deriva da grade de Hermann, pontos pretos e cinzas aparecem e desaparecem no lugar dos pontos brancos.
5. Triângulo de Kanizsa:
Na figura acima, visualiza-se um triângulo branco por cima de outras figuras geométricas. Porém, esse triângulo não está desenhado.
Outro exemplo:
6. Visualizamos um cubo na figura abaixo, que também não está desenhado.
7. Estas imagens estão paradas, não se movem.
8. O círculo central da esquerda tem o mesmo tamanho do círculo central da direita.
9. O tamanho das esferas é o mesmo. Porém, o cenário nos da a ilusão de que elas têm tamanhos diferentes.
10. Imagens ambíguas
Rostos ou cálice?
Cubo de Necker:
Qual face do cubo está na frente?
Quantos cubos há na figura abaixo? Três ou cinco?
Em qual sentido a bailarina está girando?
Essa animação é constituída por imagens ambíguas, em que a perna levantada da bailarina pode ser a da direita ou a da esquerda. Assim, o cérebro pode interpretar que a bailarina está girando no sentido horário ou no sentido anti-horário.
Para você, a bailarina está girando em qual sentido? Tente vê-la girar no sentido oposto. Se não conseguir, experimente olhar apenas para um dos pés dela e interpretar que o pé está girando no sentido contrário. Em seguida, volte a observar a bailarina inteira.
11. As linhas são paralelas.
12. Ilusão de Hering:
As duas linhas verticais estão retas.
13. Imagens impossíveis:
Triângulo de Penrose:
É um triângulo impossível, em que os três vértices não podem ser formados ao mesmo tempo.
Existem dois modelos concretos do triângulo de Penrose, que são mostrados nas duas fotos abaixo.
O modelo acima está localizado na cidade de Perth, Austrália.
Esse é o outro modelo, localizado em Ophoven, Bélgica.
Agora, veja os dois modelos de outro ângulo.
Cachoeira de Escher:
14. Os círculos são concêntricos, o que não parece.
15. Nesta figura, parece que há círculos brancos e concêntricos, que não existem.
16. O que a placa diz?
Você percebeu que a palavra NA aparece duas vezes?
17. Todas as linhas abaixo estão retas.
